Package org.gnome.graphene

package org.gnome.graphene
A thin layer of types for graphic libraries

The following native libraries are required and will be loaded: libgraphene-1.0.0

For namespace-global declarations, refer to the Graphene class documentation.

Graphene-box

graphene_box_t provides a representation of an axis aligned minimum bounding box using the coordinates of its minimum and maximum vertices.

Graphene-euler

The graphene_euler_t structure defines a rotation along three axes using three angles. It also optionally can describe the order of the rotations.

Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. The angles on each axis can be placed in a vector of three components—α, β, and γ—called the *Euler angle vector*. Each rotation described by these components results in a rotation matrix: 


   rot(α) = A
   rot(β) = B
   rot(γ) = G

The resulting rotation matrix expressed by the Euler angle vector is given by the product of each rotation matrix: 


   G × B × A = R

In order to specify the meaning of an Euler angle vector, we need to assign each axis of rotation to the corresponding α, β, and γ components, for instance X, Y, and Z.

Additionally, we need to specify whether the rotations move the axes as they are applied, also known as intrinsic, or relative rotations; or if the axes stay fixed and the vectors move within the axis frame, also known as extrinsic, or static rotations. For instance, a static rotation alongside the ZYX axes will be interpreted as relative to extrinsic coordinate axes, and be performed, in order, about the Z, Y, and finally X axis. A relative rotation alongside the ZXZ axes will be interpreted as relative to intrinsic coordinate axes, and be performed, in order, about the Z axis, about the rotated X axis, and finally about the rotated Z axis.

Finally, we need to define the direction of the rotation, or the handedness of the coordinate system. In the case of Graphene, the direction is given by the right-hand rule, which means all rotations are counterclockwise.

Rotations described Euler angles are typically immediately understandable, compared to rotations expressed using quaternions, but they are susceptible of "Gimbal lock" — the loss of one degree of freedom caused by two axis on the same plane. You typically should use graphene_euler_t to expose rotation angles in your API, or to store them, but use graphene_quaternion_t to apply rotations to modelview matrices, or interpolate between initial and final rotation transformations.

For more information, see:

  • http://en.wikipedia.org/wiki/Rotation_matrix
  • http://en.wikipedia.org/wiki/Euler_angles
  • http://mathworld.wolfram.com/EulerAngles.html
  • "Representing Attitude with Euler Angles and Quaternions: A Reference" by James Diebel, 2006
  • "Graphics Gems IV", edited by Paul Heckbert, Academic Press, 1994.

See also: graphene_quaternion_t.

Graphene-frustum

A graphene_frustum_t represents a volume of space delimited by planes. It is usually employed to represent the field of view of a camera, and can be used to determine whether an object falls within that view, to efficiently remove invisible objects from the render process.

Graphene-gobject

Graphene optionally provides information for using its own types with GObject properties and signals.

Using Graphene with GObject
In order to discover at compile time if Graphene exposes type information for the GType type system, you need to check if the graphene-gobject-1.0 pkg-config file exists.

If you're using Meson to build your project, you can use a typical dependency() object, for instance: 

  graphene_dep = dependency('graphene-gobject-1.0')

If you're using Autotools to build your project, you can use the PKG_CHECK_EXISTS m4 macro, for instance: 

  PKG_CHECK_EXISTS([graphene-gobject-1.0],
                    [action-if-found],
                    [action-if-not-found]

All the types provided by Graphene are boxed types, which means you will have to use the GBoxed API when dealing with GValue, GParamSpec, and signal marshallers. For instance, to install a property in a GObject class that uses graphene_rect_t, you can use: 

  g_object_class_install_property (object_class, PROP_BOUNDS,
     g_param_spec_boxed ("bounds", "Bounds", "Bounds of an object",
                         GRAPHENE_TYPE_RECT,
                         G_PARAM_READWRITE | G_PARAM_STATIC_STRINGS);

You'll then need to use g_value_set_boxed() and g_value_get_boxed() in order to access the graphene_rect_t pointer from the GValue data structure.

Whereas for creating a new signal that has a graphene_point_t parameter you can use: 

  signals[HIT_TEST] =
     g_signal_new ("hit-test",
                   G_TYPE_FROM_CLASS (object_class),
                   G_SIGNAL_RUN_LAST,
                   0,
                   g_signal_accumulator_true_handled, NULL,
                   marshal_BOOLEAN__BOXED,
                   G_TYPE_BOOLEAN, 1,
                   GRAPHENE_TYPE_POINT);

Using Graphene via GObject introspection
When using Graphene with another language than C, the GObject Introspection bindings change the type names to the CamelCase version of the C name, minus the _t suffix; for instance:

  • graphene_point_t becomes GraphenePoint
  • graphene_point3d_t becomes GraphenePoint3D
  • graphene_rect_t becomes GrapheneRect
  • graphene_matrix_t becomes GrapheneMatrix

There is no direct access for the low level graphene_simd4f_t and graphene_simd4x4f_t SIMD types.

Graphene-matrix

graphene_matrix_t is a type that provides a 4x4 square matrix, useful for representing 3D transformations.

The matrix is treated as row-major, i.e. it has four vectors (x, y, z, and w) representing rows, and elements of each vector are a column: 

  ⎡ m.x ⎤    ⎛ x.x  x.y  x.z  x.w ⎞
   ⎜ m.y ⎟ -\\ ⎜ y.x  y.y  y.z  y.w ⎟
   ⎜ m.z ⎟ -/ ⎜ z.x  z.y  z.z  z.w ⎟
   ⎣ m.w ⎦    ⎝ w.x  w.y  w.z  w.w ⎠

It is possible to easily convert a graphene_matrix_t to and from an array of floating point values that can be used with other libraries.

The contents of a graphene_matrix_t are private, and direct access is not possible. You can modify and read the contents of a graphene_matrix_t only through the provided API.

Conventions # {#conventions}
Graphene uses left-multiplication for all its operations on vectors and matrices; in other words, given a matrix A and a vector b, the result of a multiplication is going to be: 


   res = b × A

Multiplying two matrices, on the other hand, will use right-multiplication; given two matrices A and B, the result of the multiplication is going to be 


   res = A × B

as the implementation will multiply each row vector of matrix A with the matrix B to obtain the new row vectors of the result matrix: 


   res = ⎡ A.x × B ⎤
         ⎜ A.y × B ⎟
         ⎜ A.z × B ⎟
         ⎣ A.w × B ⎦

For more information, see the documentation for graphene_simd4x4f_t, especially the following functions:

  • graphene_simd4x4f_vec4_mul()
  • graphene_simd4x4f_vec3_mul()
  • graphene_simd4x4f_point3_mul()
  • graphene_simd4x4f_matrix_mul()

Graphene-plane

graphene_plane_t is a structure representing a plane that extends infinitely in 3D space, described using the [Hessian normal form](http://mathworld.wolfram.com/HessianNormalForm.html) of a unit length normal vector pointing towards the origin, and a constant distance from the origin along the normal vector.

Graphene-point

graphene_point_t is a data structure capable of describing a point with two coordinates:
  • graphenePointT.x
  • graphenePointT.y

Graphene-point3d

graphene_point3d_t is a data structure capable of describing a point with three coordinates:
  • graphenePoint3dT.x
  • graphenePoint3dT.y
  • graphenePoint3dT.z

Graphene-quad

A graphene_quad_t represents a coplanar, four vertex quadrilateral shape.

Graphene-quaternion

Quaternions are a mathematical entity that can be used to represent rotation transformations in 3D space; unlike the usual Euler representation with roll, pitch, and yaw, quaternions do not suffer from the so-called "Gimbal Lock" problem.

See also: graphene_euler_t

Graphene-ray

graphene_ray_t is a structure representing a ray emitted by an origin, identified by a point in 3D space, in a given direction, identified by a vector with 3 components.

A common use of graphene_ray_t is ray-casting to find which objects in a 3D scene are under the coordinates of the pointer.

Graphene-rect

graphene_rect_t is a type representing a rectangle through an origin graphene_point_t point and a graphene_size_t size.

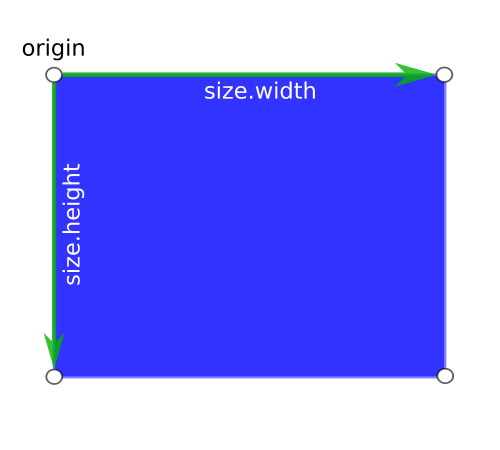
Operations on a graphene_rect_t will normalize the rectangle, to ensure that the origin is always the top-left corner of the rectangle and that the size is always positive.

Graphene-size

graphene_size_t represents a size composed of a grapheneSizeT.width by a grapheneSizeT.height.

Graphene-sphere

graphene_sphere_t provides a representation of a sphere using its center and radius.

Graphene-triangle

graphene_triangle_t represents a triangle in 3D space.

Graphene-vectors

Graphene has three vector types, distinguished by their length:

1. graphene_vec2_t, which holds 2 components x and y 2. graphene_vec3_t, which holds 3 components x, y, and z 3. graphene_vec4_t, which holds 4 components x, y, z, and w

Each vector type should be treated as an opaque data type.